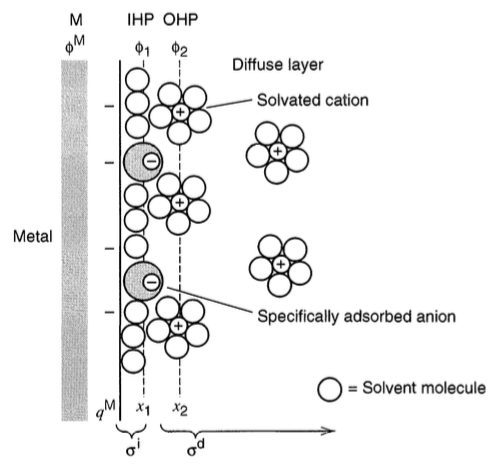
双电层建立的GCS模型
这篇文章想介绍电化学中一个很优雅的概念,并阐释这个概念如何通过建立模型而不断完善。
这个概念叫做:
双电层(electrical double layer)
假设,将一个金属片放进电解液中,那么会发生什么呢?或者更科学性的描述是:在电极与电解液的界面处,物质与电荷的分布状态是怎样的?下面选自百度百科的一段话:
在双电层两侧之间,即电子导体相与离子导体之间的电位差就是所谓的电极电位。金属浸入电解质溶液中,金属表面由于晶格畸变能较高使表面金属离子易于和溶液中极性水分子作用而发生水化。如果金属离子的水化能高于金属表面晶格的键能,一些表面金属离子将脱离金属晶格进入溶液,形成水化离子。金属表面晶格的电子由于被水分子电子壳层中的同名电荷排斥,不能随水化反应转入溶液,因此就必然有相当数量的过剩电子在金属表面积累。
由于金属表面负电荷的吸引和溶液中正电荷的排斥,进入溶液的水化金属离子不能向溶液深处扩散,而只能滞留在金属表面附近,这就阻碍了表其他金属离子继续溶解。浴液中的部分水化金属离子也可能再沉积到金属表面。当溶解于沉积速度相等的时候,就可以在该处形成一种动态平衡的电荷分布。通常把金属与电解质溶液界面处形成的这种荷电的界面偶层称为双电层。
由于双电层的形成,界面处即双电层两侧之间变产生了电位差。
(1)Helmholtz模型
首先,亥姆赫兹(Helmholtz)试图探究这个问题,他建立了一个模型,我们简称其为H模型。
H模型的核心思想是:相反的电荷等量分布于界面两侧。这也是“double layer”的由来。
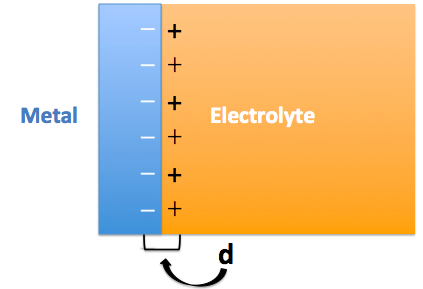
进而,这个结构可以等效为一个平板电容器,并用如下公式描述单侧的电荷密度(σ)与两层电荷间的电势差(V)的关系,其中,d为正负电荷中心的距离。

至此,H模型成功地将将一个电化学的普遍场景抽象为基本公式。
然而,该模型存在一个明显缺陷:由上式可推论出,C是一个恒定值,然而实验观测中,C是一个变量,相对电位与电解液浓度等都会对其产生影响。
比如,汞电极在NaF电解液中,测得C值如下图所示
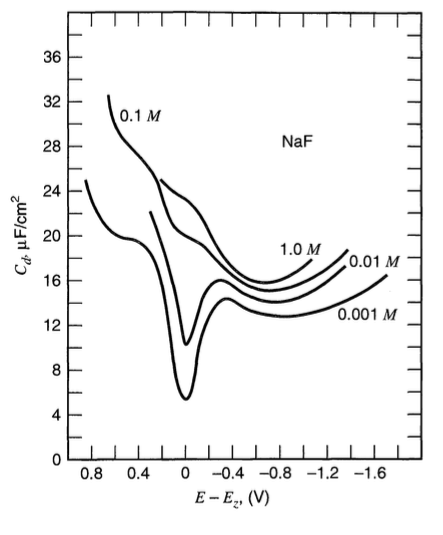
其中可以看到明显的两个趋势是:
(1)C相对于电位成V型的对称分布;
(2)电解液的浓度越高,C数值越大。
因此,一个良好双电层模型需要解释这两个现象。
(2)Gouy-Chapman模型
随后,Gouy和Chapman联手改进了这个模型,我们简称其为G-C模型。G-C模型的核心是引入了一个新的概念:扩散层(diffuse layer)
让我们回到电极与电解液的界面处,电荷在电极这一侧是严格分布于其表面。然而,在电解液这一侧却不是这样:由于不同离子间的相互作用,使得很多电荷会扩散到远离界面的体相溶液中。
因此,G-C模型可由下图近似表示,
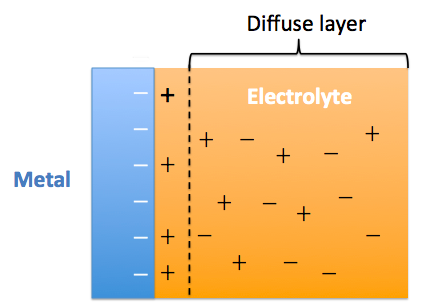
经过G-C模型的改进,原本电容公式中的d就变成了一个变量。
不难想象,当界面两侧电势差较大时,更多的离子会被压缩到靠近电极的位置;当电解液浓度高时,离子也可以在较小的空间上与电极达到电荷平衡。
经过G-C模型的改进,双电层预测NaF的水溶液作为电解液,其电容与电位及浓度关系如下,
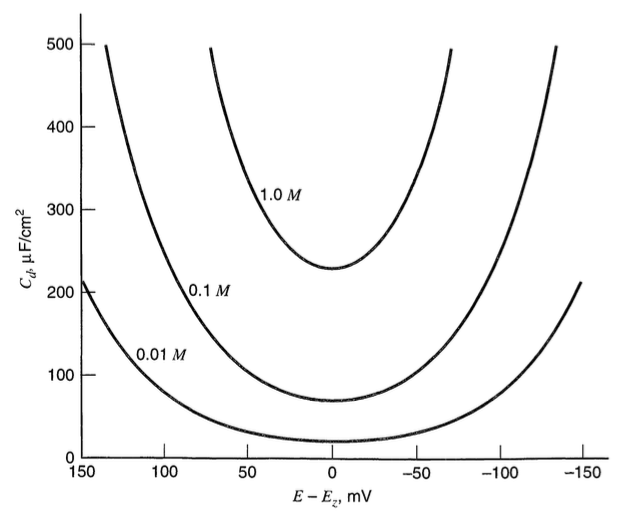
可见,经过G-C模型的改进,双电层理论对Cd变化有了很好的解释。
然而,G-C模型也是由弊端的:
(1)预测图中,在V型曲线的两端(既电位差极大处),C值趋近于无穷大。而实际测试中,在该处的C值趋向平缓;
(2)预测值远远高于实测值。
综上,我们可以说G-C模型揭示了“部分真理”,但与现实世界仍有较大偏差。
(3)Gouy-Chapman-Stern模型
G-C模型中,之所以会出现Cd无穷大的预测,是因为电荷被抽象为一个点,这也是物理学中常用的处理方法。
然而,当我们电势差很大时,这些抽象的“点电荷”会被无限压缩到接近电极表面的位置,因此正负电荷的距离d将趋紧于0,从而造成C接近无穷大。
据此,Stern在G-C模型的基础上,加入了一个新的条件:离子是有尺寸的
进而,得到下图所示的G-C-S模型。
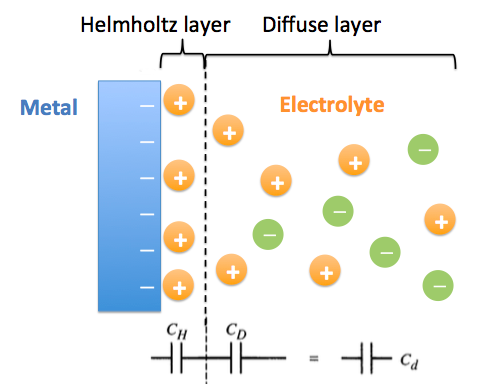
G-C-S模型中,Stern将较为紧密的内层成为亥姆赫兹层(Helmholtz layer),该层产生的电容!C_H在固定体系中为恒定值,不受电势差的影响。外层仍为扩散层,产生电容C_D。
C_H与C_D为串联,共同组成双电层电容C_d,三者关系为:
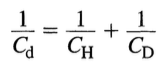
由电学知识可知,C_d永远小于C_H与C_D中的较小值。在低电势差时,C_D值很小,C_d主要受其影响,而具有V型的特征。在高电势差时,C_D值很大,而对C_d值的贡献可以忽略不计,C_d趋近于$C_H$值。
至此,G-C-S模型妥善地解决了上文中涉及的问题。然而,事情并没有结束。
(4)后续
G-C-S模型中仍然有很多未尽之处,比如:
(1)在实际情况中,电解液中的阴阳离子表面会被溶剂离子包围,电荷的载体是这种“溶剂化离子(solvated ions)”;
(2)在界面处会有吸附现象(adsorption)发生,如果吸附力大于静电力,那么即使是同种电荷也可以稳定处于界面处。
如果考虑这两点,那么,G-C-S模型的改进版将如下图所示,